STAT/MATH 395B

Solution, homework 2.

4.3.2 E(X) = (1+...+n)/n = (n+1)/2

E(X²) = (1 + 4 + ... + n²) / n = (n+1)(2n+1)/6

Var(X) = E(X²)-(E(X))² = [2(n+1)(2n+1)-3(n+1)²)/12 = (n²-1)/12

4.3.13 E(Z) = E((X-m)/s) = E(X - E(X)) / s = 0

Var(Z) = E((X - E(X))²)/s² = Var(X)/Var(X) = 1

4.3.14 (a) E(2X-3) = 2E(X)-3 = 2m-3

(b) Var(2X-3) = Var(2X) = 4 Var(X) = 4b

(c) E(X²) = Var(X) + (E(X))² = b + m²

(d) E((X-1)²) = E(X²) - 2 E(X) + 1 = b + m² - 2 m + 1 = b + (m-1)²

(e) Var(5-X) = Var(-X) = (-1)² Var(X) = Var(X) = b

(f) E((X-2)(X+1)) = E(X² - X - 2) = b + m² - m + 2

4.4.4 f(x,y) = (6/5)(x²+y), 0<x<1, 0<y<1

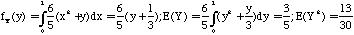
Hence Var(X)=11/25 - 9/25 = 2/25; Var(Y) = 13/30 - 9/25 = 11/150

so Cov(X,Y) = 7/20 - (3/5)² = -1/100 and Corr(X,Y) = (-1/100) / (2/25 x 11/150 )^1/2 =-.13

4.4.9 (a)

(b) Since the range of possible y-values depend on the x-value, X and Y cannot be independent.

(c) f_X,Y(x,y) = 1/2, |x|+|y| < 1

(d)

(e)

(f) f_Y(y)=f_X(y); E(Y)=E(X), Var(Y)=Var(X) by symmetry

(g) by symmetry, so Cov(X,Y) = Corr(X,Y) = 0. Two random variables can be uncorrelated without being independent.

4.4.12 Cov(X+Y,X-Y) = Cov(X,X) - Cov(X,Y) + Cov(Y,X) - Cov(Y,Y) = Var(X) - Var(Y) = 0 if Var(X) = Var(Y).