Graphical Markov Models in Multivariate Analysis

Participating Faculty: M. Perlman, T. Richardson

Graduate Students: S. Chaudhuri, M. Drton

A central aspect of statistical science is the assessment of dependence among stochastic variables. The familiar concepts of correlation, regression, and prediction are special cases, and identification of causal relationships ultimately rests on representations of multivariate dependence. Graphical Markov models (GMM) use graphs, either undirected, directed, or mixed, to represent multivariate dependences in a visual and computationally efficient manner. A GMM is usually constructed by specifying local dependences for each variable, equivalently, node of the graph in terms of its immediate neighbors and/or parents by means of undirected and/or directed edges. This simple local specification can represent a highly varied and complex system of multivariate dependences by means of the global structure of the graph, thereby obtaining efficiency in modeling, inference, and probabilistic calculations. For a fixed graph, equivalently model, the classical methods of statistical inference may be utilized. In many applied domains, however, such as expert systems for medical diagnosis or weather forecasting, or the analysis of gene-expression data, the graph is unknown and is itself the first goal of the analysis. This poses numerous challenges, including the following:

The numbers of possible graphs and models grow superexponentially in the number of variables.
Distinct graphs G may be Markov equivalent = statistically indistinguishable.
Conversely, the same graph may possess different Markov interpretations.

Chain graphs (Perlman)

A main goal of this research project is to facilitate statistical inference for model structure for chain graphs (Figure 1), which allow both undirected and directed edges in order to represent associative and causal relations, respectively. D. R. Cox has stated that chain graphs represent ``a minimal level of complexity needed to model empirical data. Andersson, Madigan, and Perlman have introduced an alternative Markov property (AMP) for chain graphs that conforms more closely to the Markov property associated with the well-known subclass of directed acyclic graphs (DAG).

Fig. 1. Structure of a chain graph

Current projects:

fully characterize Markov equivalence classes of AMP chain graphs via their essential graphs;
devise efficient methods for model selection and testing;
develop methods of inference for models comprising submodels of varying dimensionalities;

Recent Publications

Alternative Markov properties for chain graphs. Andersson, S., Madigan, D., and Perlman, M. Scandinavian Journal of Statistics 28, 33-85, 2001.

Conditional independence models for seemingly unrelated regressions with incomplete data. Drton, M., Andersson, S., and Perlman, M. Tech. Report No. 431, Dept. of Statistics, University of Washington, Seattle, 2003.

On the bias and mean-square error of order-restricted maximum likelihood estimators. Chaudhuri, S. and Perlman, M. D. Journal of Statistical Planning and Inference, to appear. 2004.

A SINful approach to model selection for gaussian concentration graphs Drton, M. and Perlman, M. Tech. Report No. 429, Dept. of Statistics, University of Washington, Seattle. Biometrika, to appear, 2004.

Pathwise separation and completeness for AMP chain graph Markov models. Annals of Statistics, Levitz, M., Perlman, M. D., and Madigan, D. 29, 1751-1784, 2001.

Ancestral graphs (Richardson)

The goal of many studies is to gain insight into the process which generated a given set of data. Directed acyclic graph models (DAGs) have the advantage that they have a simple causal interpretation. However, if some of the variables in a causal data-generating process are unobserved then an analysis based on DAGs involving only the observed variables can be highly misleading. In particular, there may be spurious dependencies that are induced by the hidden variables. It is often impossible to use DAG models which directly include such hidden variables since these models are not in general identified.

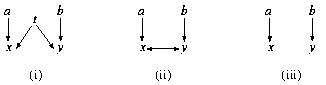
Fig. 2. (i) a simple DAG model; (ii) the ancestral graph resulting from marginalizing over t; (iii) the ancestral graph resulting from conditioning on t

An alternative approach uses a richer class of graphs, called ancestral graphs . These graphs directly represent the independence structure among the observed variables that may be induced by hidden variables. Additional motivation for this class derives from the causal interpretation of DAG models.

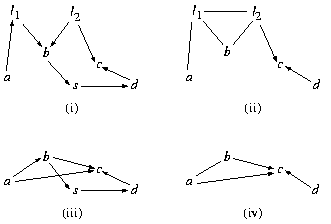
Fig. 3. (i) a DAG model; (ii) conditioning on s; (iii) marginalizing over l1 and l2; (iv) conditioning on s and marginalizing over l1 and l2.

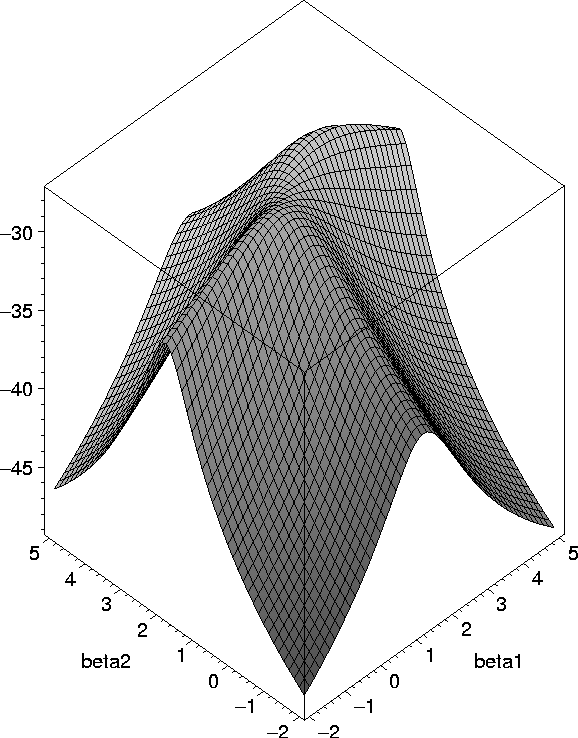
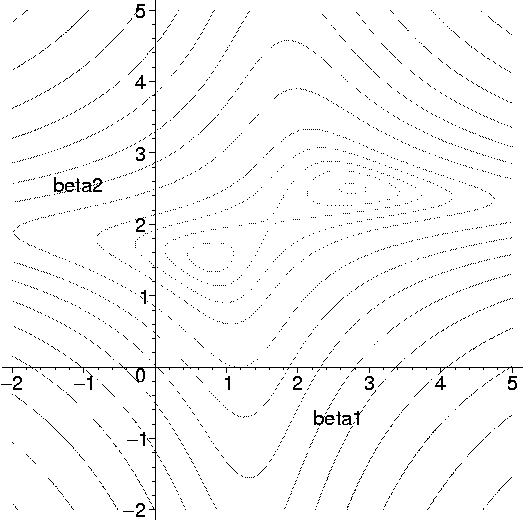
Recent work has made using this class of models practical in the multivariate Gaussian case by developing iterative fitting algorithms, implemented in the "ggm" R package.

Fig. 4. Multimodal likelihood associated with the Gaussian ancestral graph in Fig. 2(ii)

Current research projects:

Extend the Gaussian fitting algorithms to the discrete data case;
Analyze likelihoods associated with ancestral graph models; it is known that in some situations the likelihood can be multi-modal. See Figure
Graphical analysis of non-independence constraints associated with hidden variable models;
Characterization of Markov equivalence classes of ancestral graph models;
Graphical analysis of the strength of dependence in DAG models.

Recent Publications

Ancestral graph Markov models Thomas Richardson and Peter Spirtes. Annals of Statistics, 2002.

Multimodality of the likelihood in the bivariate seemingly unrelated regression model Mathias Drton and Thomas Richardson. To appear in Biometrika, 2004

Causal inference via ancestral graph Markov models (with discussion). Thomas Richardson and Peter Spirtes. In Highly Structured Stochastic Systems P.J. Green, N.L. Hjort and S. Richardson (eds.).

A new algorithm for maximum likelihood estimation in Gaussian graphical models for marginal independence. Mathias Drton and Thomas Richardson. Proceedings of the Nineteenth Conference on Uncertainty in Artificial Intelligence, 2003

Iterative Conditional Fitting for Gaussian Ancestral Graph Models Mathias Drton and Thomas Richardson. Department of Statistics Technical Report No. 437

Using the structure of d-connecting paths as a qualitative measure of the strength of dependence. Sanjay Chaudhuri and Thomas Richardson. Proceedings of the Nineteenth Conference on Uncertainty in Artificial Intelligence, 2003

Markov Equivalence Classes for Maximal Ancestral Graphs Ayesha Ali and Thomas Richardson, Proceedings of the Eighteenth Conference on Uncertainty in Artificial Intelligence, 2002.

This material is based upon work supported by the National Science Foundation under Grant Nos (DMS 9972008) and (DMS 0071818). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.