I MOVED!

Find me at University of Waterloo
Recruiting MS students interested in Statistical Machine Learning!

OVERVIEW

I work on machine learning by probabilistic methods and reasoning in uncertainty. In this area, it is particularly important to develop computationally aware methods and theories. In this sense, my research is at the frontier between the sciences of computing and statistics. I am particularly interested in combinatorics, algorithms and optimization, on the computing side, and in solving data analysis problems with many variables and combinatorial structure.
Slides on my current research in Validation beyond Visualization in clustering and non-linear dimension reduction. A short overview of recent research from a prospective student's point of view is here.

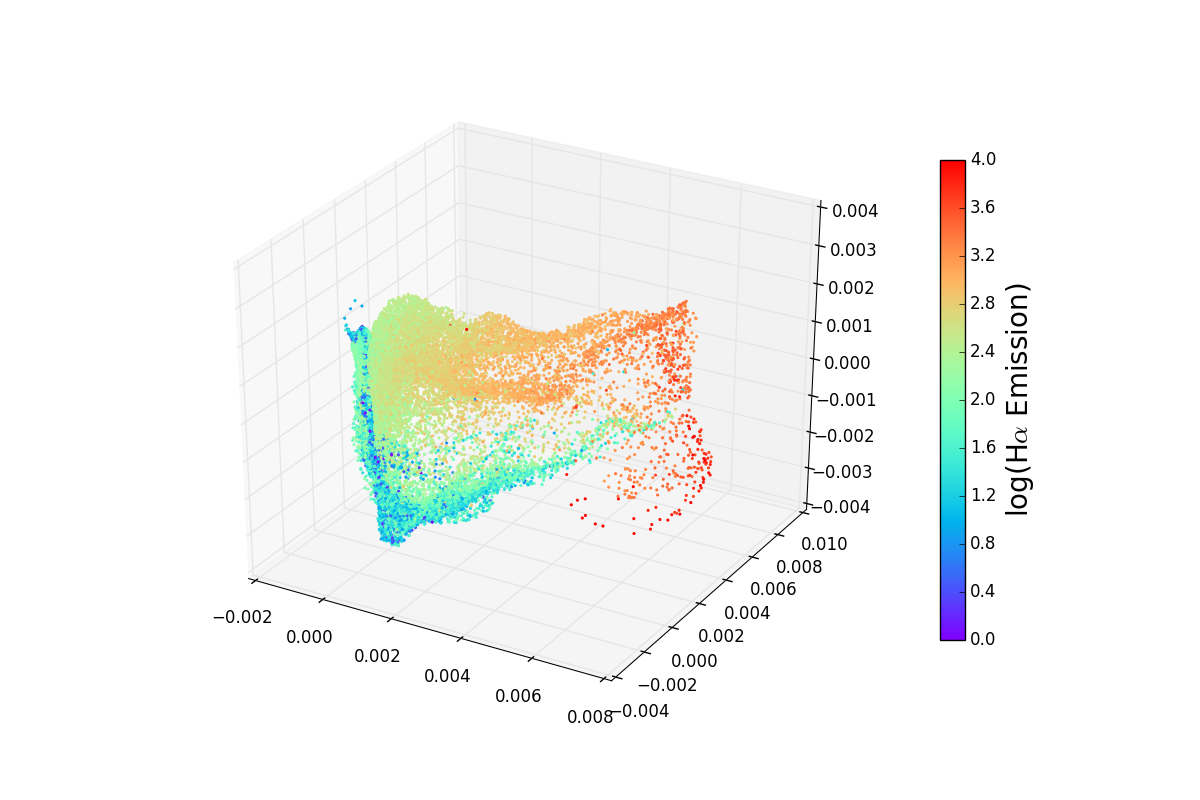MANIFOLD LEARNING AND GEOMETRIC DATA ANALYSIS

Manifold learning algorithms find a non-linear representation of high-dimensional data (like images) with a small number of parameters. However, all such existing methods deform the data (except in special simple cases). We construct low-dimensional representations that are geometrically accurate under much more general conditions. As a consequence of the kind of geometric faithfulness we aim for, one should be able to do regressions, predictions, and other statistical analyses directly on the low-dimensional representation of the data. These analyses would not be correct in general, if one were not preserving the original data geometry accurately.

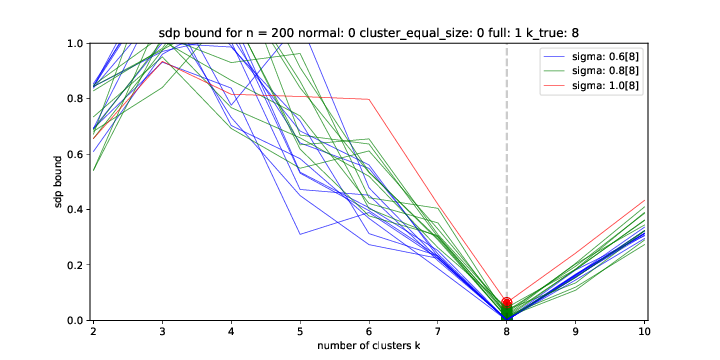
FOUNDATIONS OF CLUSTERING

It was widely believed that little can be theoretically said about clustering and clustering algorithms, as most clustering problems are NP-hard. This part of my work aims to overcome these difficulties, and takes steps towards developing a rigurous and practically relevant theoretical understanding of the clustering algorithms in everyday use. A fundamental concept is that of clusterability of the data. Given that the dat contains clusters, one can show that: we can devise initialization methods that lead w.h.p. to an almost correct clustering, we can prove that a given clustering is almost optimal, and that if the nubmer of clusters in the data is smaller than our guess, we will obtain unstable results.

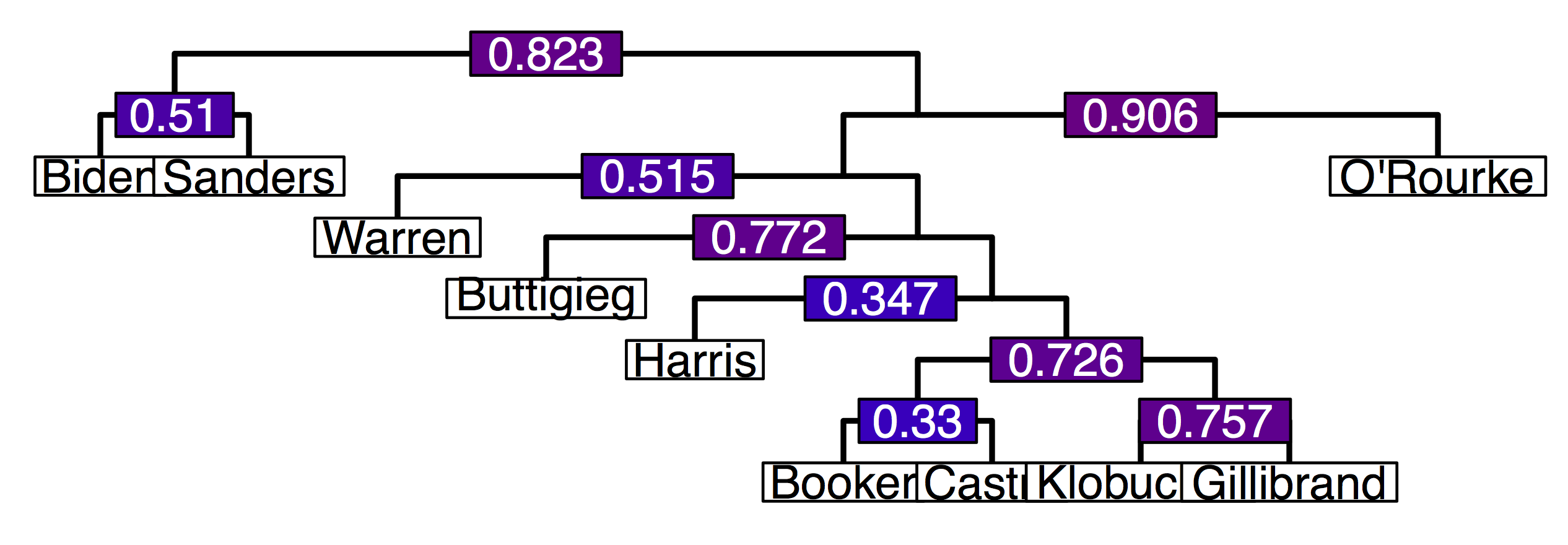PERMUTATIONS, PARTIAL RANKINGS, INTRANSITIVITY AND CHOICE

It has been often noted that people's choices are not transitive: in other words, their preferences between K objects are not consistent with an ordering. Economic theory of choice has introduced various theories explaining how the observed intransitivity may arise. However, there is no work to date on how one may infer these models from data. Among the things I want to do: to formulate estimation problems for the hidden context and other models of intransitivity that are relevant to practical domains; to define when the model is identifiable (it may not be when the number of components K is large) and to design rigorously founded algorithms to estimate it. More

CLUSTERING BY EIGENVALUES AND EIGENVECTORS

...is a technique rooted in graph theory for finding groups (or other structure) in data. It already has applications in image segmentation, web and document clustering, social networks, bioinformatics and linguistics. My recent work concentrates on the study of asymmetric links, or, in other words, of directed graphs. More

GRAVIMETRIC INVERSION WITH SPARSITY CONSTRAINTS

This works deals with recovering the shape of an unknown body from gravity measurements. As a mathematical physics problem, this one is old, well-studied, and one of the hardest type of inverse problems. My team is interested in finding algorithmic solutions, under realistic scenarios, that recover given features of the unknown underground density in noise. We showed that this problem can be mapped to a linear program with sparsity constraints, for which we formulated various continuous and integer approaches. The methodological and theoretical work on this problem continues, as we exploit the connections with Compressed Sensing, QBPs and submodularity. The practical results led to intriguing new research questions, since the restricted isometry assumptions that usually underlie compressed sensing algorithms can be proved not to hold for the gravimetry problem. (Collaboration with Caren Marzban and Ulvi Yurtsever.)

PROTEOMICS

Interpreting the very complex signature of an amino-acid sequence that is subjected to collision induced dissociation (CID). Probabilistic identification of the protein composition of a complex mixture from high throughput mass spectrometry data.